DEFINICIÓN
Una ecuación diferencial es una ecuación que involucra derivadas (o diferenciales) de una función desconocida de una o más variables. Si la función desconocida depende sólo de una variable, la ecuación se llama una ecuación diferencial ordinaria. Sin embargo, si la función desconocida depende de más de una variable la ecuación se llama una ecuación diferencial parcial.
Un ejemplo de ecuación diferencial ordinaria es:

La variable independiente (v. i) es x
La variable dependiente (v. d) es y
Un ejemplo de ecuación diferencial parcial es:

La variable independiente (v. i) es "x" y "y"
La variable dependiente (v. d) es V
1.2) ORDEN DE UNA ECUACIÓN DIFERENCIAL
El orden de una ecuación diferencial está dado por el orden mayor de su derivada.
Ejemplo
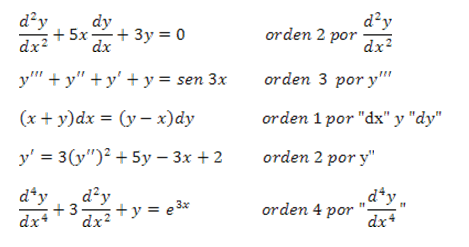
1.3) GRADO DE UNA ECUACIÓN DIFERENCIAL
El grado de una ecuación diferencial está dado por el exponente del mayor orden de su derivada.
Ejemplos
Determinar el orden y grado de las siguientes ecuaciones diferenciales ordinarias.
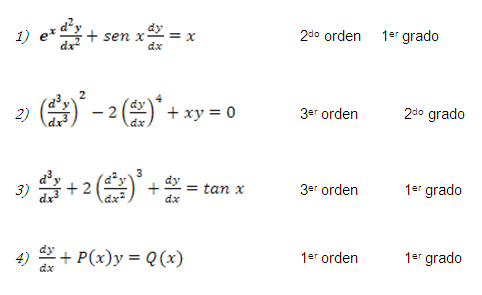
Solución de una ecuación diferencial
Una función que cuando se remplaza en la ecuación diferencial da una igualdad, se llama una solución de la ecuación diferencial, por lo tanto, resolver una ecuación diferencial es encontrar una función desconocida que al ser sustituida en la ecuación diferencial se obtiene una igualdad.
2.1) FUNCIÓN PRIMITIVA DE UNA ECUACIÓN DIFERENCIAL
Es una expresión equivalente a la ecuación diferencial que carece de derivadas.
Ejemplo:
Resolver la ecuación diferencial

La expresión es una "función primitiva" de la ecuación diferencial.
Verificación

Observación: Al derivar la función primitiva se reproduce exactamente la ecuación diferencial.
2.2) PROBLEMA DE VALOR INICIAL
Un problema de valor inicial es un problema que busca determinar una solución a una ecuación diferencia sujeta a condiciones sobre la función desconocida y sus derivadas especificadas en un valor de la variable independiente. Tales condiciones se llaman condiciones iniciales.
Un problema de valor de frontera es un problema que busca determinar una solución a una ecuación diferencia sujeta a condiciones sobre la función desconocida especificadas en dos o más valores de la variable independiente. Tales condiciones se llaman condiciones de frontera.
Ejemplo ilustrativo
Una curva tiene la propiedad de que su pendiente en cualquier punto (x,y) de ella es igual a 2x. Hallar la ecuación de la curva si ésta pasa por el punto (2,5)
Solución:

2.3) DESCRIPCIÓN DE UNA FAMILIA DE CURVAS

Ecuaciones diferenciales ordinarias de primer orden
3.1) ECUACIONES CON VARIABLES SEPARABLES
Encuentre la solución general de la ecuación diferencial.

Resolución.

Soluciones Particulares

Graficando en Graph

Comprobación

3.2) ECUACIONES HOMOGÉNEAS
Es homogénea si no contiene términos que dependen únicamente de su variable independiente, en caso contrario es No Homogénea.
Ejemplos:

Ejemplo ilustrativo
Resolver la ecuación:

Resolución:
En una ecuación diferencial homogénea se realiza el cambio

Integrando

Graficando para un valor arbitrario C = 1

3.3) ECUACIONES EXACTAS
Resolver la ecuación

Resolución
Para que la ecuación diferencial sea exacta debe cumplir la condición

Como cumple la condición se trata de una ecuación diferencial exacta

Se Iguala las dos derivadas con respecto a y.

Graficando la solución de la ecuación diferencial para C = 1

3.4) ECUACIONES CON FACTORES INTEGRANTES

Una vez obtenida la nueva expresión se puede resolver la ecuación mediante los procedimientos para ecuaciones diferenciales exactas
Para obtener los factores de integración se pueden emplear las siguientes reglas:

Ejemplo ilustrativo: Resolver la siguiente ecuación diferencial

Solución
Se debe verificar si la ecuación diferencial es exacta. Las funciones definidas para las ecuaciones diferenciales exactas son:

Debido a que las 2 derivadas parciales no son iguales, la ecuación diferencial no es exacta.
Como la diferencias entre las 2 derivadas cruzadas dividida para N es una función de "x" se aplica:

Multiplicando la ecuación diferencial por el factor de integración "x" se tiene una ecuación diferencial equivalente

Debido a que las 2 derivadas parciales son iguales, la nueva ecuación diferencial es exacta.
Como la nueva ecuación diferencial es exacta se procede a resolverla como en casos anteriores. Esta solución queda como tarea para el lector.

3.5) ECUACIONES LINEALES
Resolver las siguientes ecuaciones lineales

Solución

Es una ecuación lineal en "y"
Como la solución es

Graficando para un valor arbitrario de C = 1


Es una ecuación lineal en "x"
Como la solución es

Propiedad conmutativa en los exponentes

Graficando para un valor arbitrario de C = 1

ENLACES:
https://www.youtube.com/watch?v=v3CsjgKeB7U
http://www.monografias.com/trabajos97/introduccion-ecuaciones-diferenciales-teoria-y-ejemplos-resueltos/introduccion-ecuaciones-diferenciales-teoria-y-ejemplos-resueltos.shtml
No hay comentarios.:
Publicar un comentario